2024年よりNISA制度が改正され、資産運用が非常に身近な存在となってきました。NISAなどを活用して資産運用を考えるとき、投資成果がどのようになるのか非常に気になると思います。
そこで、本記事では資産運用において将来の資産がどのようになるのかをシミュレーションするにあたって重要な複利計算をわかりやすく解説し、便利な４つの投資の法則についてもご紹介します。

複利とは？計算方法は？

金利やリターンを考える際には、単利と複利の違いを理解することが重要です。
単利とは、元本のみに利子が発生することを意味します。
複利とは、元本に加えて利子にも利子がつくため、利子がさらに利子を生むことを意味します。
例えば、投資元本が100万円で、5年間の利率が年率10％の場合、投資結果がいくらになるのか単利と複利の違いを見てみましょう。

〈単利の場合〉

単利の場合、元本に対してのみ利子が発生するため、計算は比較的容易です。

1年間の利子：100万円×10％＝10万円
利子の合計：10万円×5年＝50万円
合計：150万円

〈複利の場合〉

複利の場合、利子に対しても利子が発生するため、単利と比べると計算は複雑です。

1年目の利子：100万円×10％＝10万円
2年目の利子：110万円×10％＝11万円
3年目の利子：121万円×10％＝12万1,000円
4年目の利子：133.1万円×10％＝13万3,100円
5年目の利子：146.41万円×10％＝14万6,410円
合計：161万510円

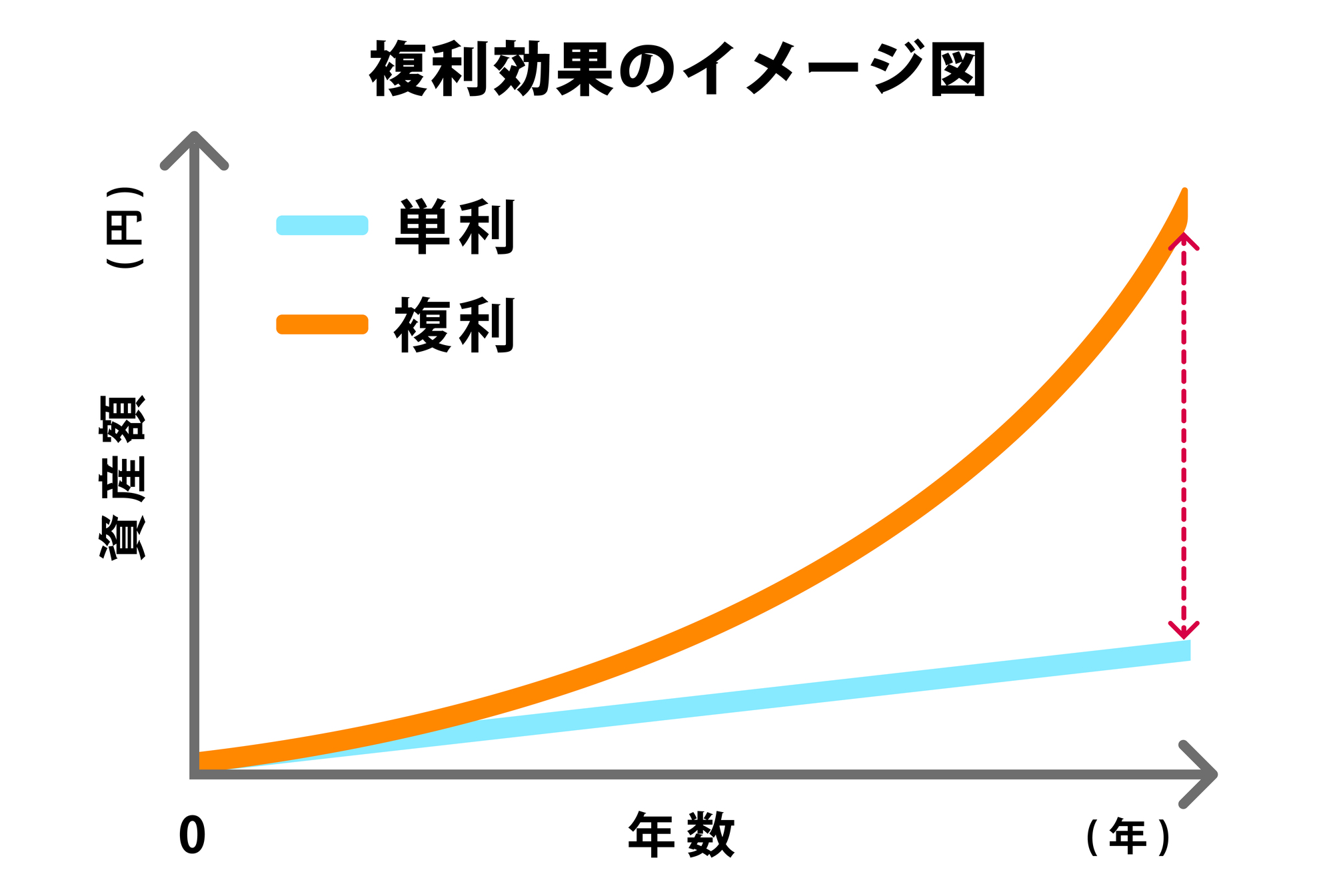
単利と比較した場合、複利のほうが2年目以降の利子が大きくなります。また、複利の利子は年々大きくなっていることがわかります。複利運用では期間が長くなるほど得られる複利効果が大きくなることから、長期投資がより重要となってきます。

一般的に資産運用のサイトなどで年利OO％、年率OO％などの記載がありますが、基本的には複利計算の数値となっていることが多いです。しかしながら、単利と比較した場合、複利計算は複雑で暗算が難しいケースが多いかと思います。
今回の例の場合、一つの式に直すと「100万円×（1＋10％）5＝161万510円」となり、Excelや計算機を使えば簡単に計算できるものではありますが、やはり暗算で答えを出すのは難しいのではないでしょうか。

そこで、ここからは知っておくと簡便なシミュレーションをする際に便利な法則を4つご紹介します。

72の法則

まずは、複利計算の法則で最も有名な数値である「72の法則」です。
これは、複利で運用した場合に投資元本が倍になるまでの年数を計算するための法則です。具体的には、以下の計算式となります。

「72÷利回り（％）＝投資元本が2倍になる期間」

（例）
年率1％の場合：72÷1＝72　約72年
年率5％の場合：72÷5＝14.4　約14.4年
年率10％の場合：72÷10＝7.2　約7.2年

投資元本100万円を年率5％で運用した場合、約14.4年後に倍の200万円になります。上記の例のように、「72の法則」を使うことで、投資金額が何年で倍になるのかという目安を知ることができます。知っていると非常に便利な数値ですので、ぜひ覚えていただきたい法則です。

126の法則

続いて「126の法則」です。
先ほどの「72の法則」は一括投資をした場合で、投資元本が倍になるまでの期間を計算する方法でした。今回の「126の法則」は、積立投資をした場合に投資元本が2倍になるまでの期間を計算するための法則です。 計算方法は「72の法則」と同様で以下のとおりです。

「126÷利回り（％）＝投資元本が2倍になる期間」

（例）
年率1％の場合：126÷1＝126　約126年
年率5％の場合：126÷5＝25.2　約25.2年
年率10％の場合：126÷10＝12.6　約12.6年

毎月5万円の積立投資が年率5％で運用できた場合、約25.2年後の投資元本は1,510万円（25年2ヵ月分で計算）で、資産合計は3,020万円になるという計算です。
積立投資で投資元本を倍に増やしたいと考えた場合、年率1％や2％では倍になるまでにそれぞれ約126年、約63年とかなり時間がかかることから、例えば、現役時代の約40年間で達成したいと考えるのであれば、少なくとも年率3％以上のリターンが必要と分かります。無理にリスクをとるべきではありませんが、参考情報として役立つでしょう。

筆者は資産運用において一番大事なことは継続することだと考えています。積立の金額が自分の生活に無理を生じさせないこと。自分が取れるリスクをしっかり把握したうえで、投資対象を選ぶこと。そして、資産運用を始める時点で、運用資産が倍になるまでにどの程度の期間がかかるのかを把握しておくなど、目標達成までの道のりを見据えることは資産運用を継続するうえでとても大切なことだと思います。
ぜひこの「126の法則」も覚えていただければと思います。

115の法則

続いて「115の法則」です。これは、最初に紹介した「72の法則」の応用編です。
一括投資をした場合、投資元本が倍になる期間を計算するのが72でしたが、投資元本が3倍になる期間を計算するものが「115の法則」です。

（例）
年率1％の場合：115÷1＝115　約115年
年率5％の場合：115÷5＝23　約23年
年率10％の場合：115÷10＝11.5　約11.5年

投資元本100万円を年率5％で運用した場合、約23年後に3倍の300万円になります。
まずは「72の法則」を覚えたうえで、余裕があればこちらも知っておくと、いろいろと考える際に応用が利くのではないかと思います。

190の法則

最後に「190の法則」です。
これは、「126の法則」の応用編で、積立投資をした場合に投資元本が3倍になるまでの期間を計算するための法則です。

（例）
年率1％の場合：190÷1＝190　約190年
年率5％の場合：190÷5＝38　約38年
年率10％の場合：190÷10＝19　約19年

積立投資で元本が3倍となるには仮に年率10％という非常に高いリターンが実現できたとしても、かなりの時間がかかることがわかります。この「190の法則」も余裕があれば覚えていただきたいと思います。

まとめ

いかがでしたでしょうか。
複利計算は考え方が複雑ですが、これらの法則を知っていれば、比較的簡単な計算で投資元本が2倍や3倍になるまでの期間を把握できます。これらの法則を活用し、長期的な視点を持ち、資産運用を継続することが投資の成功のカギではないかと思います。 本記事が少しでも皆さまのお役に立てば幸いです。

【Facebook】
わらしべ瓦版の他、投資に役立つ動画やレポートのリリース情報などを配信中！
↓下のボタンからフォローをお願いします